This post was inspired by my colleague SAO student, who asked on how we can measure stellar distances for stars which are so far away that their parallaxes are not measurable yet.
For stars more than 1000 pc away parallaxes are not measurable yet, so the only way to estimate distances is using photometry. The connection between star brightness and its distance is known as the inverse-square-law (Equation 1.).
B=(L/2Pid2)
dL=(L/4PiB)1/2
Where, B is the star’s apparent brightness, L is its luminosity (W m-2),
d is its distance to an observer.
Equation 1. needs to be changed if one takes into account the expansion of the Universe, but this is irrelevant for all stars in our Local Group.
We can measure the star’s apparent brightness B; then assume the star’s luminosity L; and then solve Equation 1. for the object's luminosity distance dL. The problem is that we can only measure star’s brightness B and its apparent magnitude m, while the luminosity and absolute magnitude must be derived in some way.
There are two methods for deriving luminosities – one uses spectroscopic parallaxes and another uses standard candles.
Both methods use distant-independent properties of stars, which make them good techniques for distance measurements.
A distance-independent property is the property of star, which doesn’t depend on its distance from an observer. For example, a period for a variable star is a distant-independent property. Star’s spectrum can serve as a distant-independent property. The later, however, is not fully distance-independent and works well only up to 100 000 pc given the current technology level.
Spectroscopic parallaxes
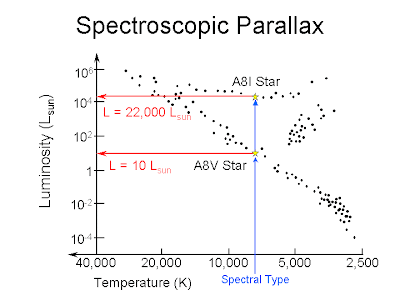
The spectroscopic parallax method uses the observed spectrum of the star as a distance-independent property to derive its luminosity (Figure 1). It involves the following steps:
1. Choose a star of interest;
2. Plot a calibrated Hertzsprung–Russell (H-R) diagram for nearby stars with known parallax distances;
3. Observe spectrum of the star of interest;
4. The spectral type (OBAFGKML) and luminosity class (I-V) provide the star’s unique location on a calibrated H-R diagram;
5. Once the star’s position on the H-R diagram is known, we can deduce its absolute magnitude (M).
Figure 1. Spectroscopic parallax. Image, courtesy of Prof. Richard Pogge, Ohio State Univ. As soon as we derived m from measurements and M from the H-R diagram, we can use the distance modulus (Equation 2.) to find the distance to the star - d, in parsecs.
However, the spectroscopic parallax method suffers uncertainties, which range from about 0.7 up to 1.25 absolute magnitudes, which in turn gives a factor of 1.4 to 1.8 variation in the distance (ScienceVaultWeb 2010):
· The assumption was made that the spectra from distant stars of interest are the same as spectra from nearby stars.
· Due to difficulties in observing spectra, it works up to 100 000 pc only.
· Interstellar dust can scatter the different frequencies in different ways, making the identification of spectral class even harder.
· Matter between the star and the observer would absorb some of the light and make the star's apparent brightness less than it should be.
· The star’s location on H-R diagram depends on its composition and luminosity class, which is difficult to determine for distant stars due to faint spectra. And there are many stars, which don't belong to the Main Sequence.
Spectroscopic parallaxes, however, work well for star clusters, where one can average out many measurements. Since all of the stars in the cluster are the same distance away from us, all of them will have an equal displacement along the Luminosity axis on H-R diagram. Therefore, the cluster's Main Sequence will appear to be shifted vertically in the H-R diagram from the nearby stars. Now, we can measure how much we have to shift the entire set of nearby stars so that they overlap the Main Sequence of the cluster, and can estimate how far away the cluster is.
The distances to the closest clusters, e.g. Hyades (46.34 pc), Pleiades (135 pc) can be measured directly using the parallax method (Perryman et al. 1998, HipparcosESAWeb). Once nearby open cluster distances are determined, they can be used to estimate the distances to other open clusters, up to 10—15 kpc away. Once the distances to Pleiades is determined, the distance to a Cepheid Variables can be calibrated (Popowski and Gould 1998; Percival, Salaris and Kilkenny, 2003).
This is important: since the only directly measurable distances in astronomy are those made by trigonometric parallax, the results from other techniques should be calibrated using parallax data.
Cepheids and RR Lyrae stars as standard candles
Cepheids and RR Lyrae are variable stars whose brightness varies regularly with a characteristic, periodic pattern. Period of their brightness variations is a distance-independent property and can be used for estimating distances to these stars.
Cepheids are located in the upper part of the instability strip in the H-R diagram, while RR Lyrae in the lower part. Most massive stars enter the instability strip and become variable after they have left the main sequence (Figure 2.)
In 1912 Henrietta Leavitt (1868—1921) published the results of her study of variable stars in the Large and Small Magellanic Clouds. She found that the fainter Cepheids have shorter pulsating periods. Because all Cepheids in a Magellanic Cloud are at the same distance from us, Leavitt concluded that the more luminous Cepheids pulsated more slowly.
In 1950's astronomers found that there are actually two types of Cepheids:
1. Type I or classical Cepheids are from young high-metallicity stars and are about 4 times more luminous than Type II;
2. Type II or W Virginis Cepheids.
Type I Cepheids are young high-metallicity stars 4 times more luminous than Type II Cepheids. Application of the classical Cepheid P-L relation to W Virginis Cepheids may lead and did lead to a large overestimation of the distances.
Figure 2. Cepheids and RR Lyrae on H-R diagram – the instability strip. Cepheids and RR Lyrae are variable stars whose brightness varies regularly with a characteristic, periodic pattern. Period of their brightness variations is a distance-independent property and can be used for estimating distances to these stars. Cepheids are located in the upper part of the instability strip in the H-R diagram, while RR Lyrae in the lower part. Most massive stars enter the instability strip and become variable after they have left the main sequence. Figure credit: ScienceVaultWeb. How this method works:
1. Photometric observations provide the apparent magnitude values for the variable star.
2. Plotting apparent magnitude values from observations at different times against phase (or time) creates a light curve.
3. From the light curve and the photometric data the average apparent magnitude, m, of the star and its period in days can be obtained.
4. The mean absolute magnitude, M, can be obtained by interpolating on the period-luminosity plot.
5. Once apparent magnitude, m, and absolute magnitude, M are known we can simply substitute in to the distance-modulus to obtain the distance to the star.
The question arises “How precise we can measure the period-luminosity (P-L) relation for a given star?”
Baade-Wesselink Method
The classical method that derives the distance of a pulsating star by comparing its linear radius variation, estimated from the radial velocity curve, with its angular radius variation, which can be estimated from the light curve. The method is named after Walter
Baade and the Dutch astronomer Adriaan Jan Wesselink (1909–1995).
The recent advances in interferometry and observational techniques allowed the direct detection of pulsations in nearby Cepheids and RR Lyrae, providing an independent distance measurement of pulsating stars (Cox 1980, Marengo et al. 2004).
Issues with using distance measurement techniques for Cepheids and RR Lyrae
Studies show that in estimating distances using P-L relation an individual Cepheid could deviate up to ± 0.6 mag in B. Such an error if applied to an individual star would end up into an error of about 30% in distance (CaltechCepheidsWeb 2010). Therefore, large samples needed to decrease the error.
The error on the apparent modulus decreases inversely with the square root of the number of samples, so decreasing an error from 30% to 10% is possible with a sample containing a dozen Cepheids.
The other issues include the systematic effects of reddening and the systematic effects of metallicity,.
Interstellar dust absorbs light, particularly at blue wavelengths. This dust absorption can lead to erroneous luminosity-color determinations, so a Cepheid from an external galaxy will appear both –fainter and more distant and redder and cooler – than it actually is. Systematic errors due reddening, if not corrected, will affect the distance scale.
The role of metallicity in the evolution of individual Cepheids and how it affects P-L relation and classic B-W method has been a matter of debate for several decades. Gieren et al. (1998, 2005) found a significantly different slope between the Galactic and LMC samples of Cepheids based on ISB analysis of Galactic and LMC Cepheids.
Trigonometric parallaxes for RR Lyrae were determined by HIPPARCOS and HST. However, only data for RR Lyr and 2 others were considered to be accurate enough (Benedict et al., 2002, Carretta and Gratton 2000).This makes calibration for P-L and B-W methods difficult.
References:
BENEDICT et al., 2002, ASTROMETRY WITH THE HUBBLE SPACE TELESCOPE: A PARALLAX OF THE FUNDAMENTAL DISTANCE CALIBRATOR RR LYRAE, THE ASTRONOMICAL JOURNAL, 123:473-484
Carretta and Gratton 2000, Distances, Ages, and Epoch of Formation of Globular Clusters, The Astrophysical Journal, 533:215-235
Carretta, Gratton, Clementini, 2000, Mon. Not. R. Astron. Soc. 316, 721±728 (2000)
Gieren, W.P., Fouque, P., & Gomez, M.; 1998, AJ, 496, 17
Gieren, W., Storm, J., Barnes, T.G., et al.; 2005, ApJ, 627, 224
Marengo M., Karovska M., Sasselov D., 2004, AN ERROR ANALYSIS OF THE GEOMETRIC BAADE-WESSELINK METHOD, The Astrophysical Journal, 603:285–291
Perryman et al., 1998, The Hyades: distance, structure, dynamics, and age, arXiv:astro-ph/9707253
ScienceVaultWeb- http://sciencevault.net/ibphysics/astrophysics/stellardistances.htm
Carretta, E., Gratton, R., Clementini, G., & Fusi Pecci, F. (2000). Distances, Ages, and Epoch of Formation of Globular Clusters The Astrophysical Journal, 533 (1), 215-235 DOI: 10.1086/308629